Context Free Gramma
Just a reference from here http://en.wikipedia.org/wiki/Context-free_grammar
A context-free grammar G is defined by the 4-tuple
 where
where
 is a finite set; each element
is a finite set; each element  is called a non-terminal character or a variable. Each variable represents a different type of phrase or clause in the sentence. Variables are also sometimes called syntactic categories. Each variable defines a sub-language of the language defined by
is called a non-terminal character or a variable. Each variable represents a different type of phrase or clause in the sentence. Variables are also sometimes called syntactic categories. Each variable defines a sub-language of the language defined by 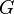 .
. is a finite set of terminals, disjoint from
is a finite set of terminals, disjoint from  , which make up the actual content of the sentence. The set of terminals is the alphabet of the language defined by the grammar
, which make up the actual content of the sentence. The set of terminals is the alphabet of the language defined by the grammar 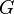 .
.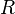 is a finite relation from
is a finite relation from  to
to 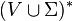 , where the asterisk represents the Kleene star operation. The members of
, where the asterisk represents the Kleene star operation. The members of 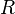 are called the (rewrite) rules or productions of the grammar. (also commonly symbolized by a
are called the (rewrite) rules or productions of the grammar. (also commonly symbolized by a 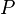 )
)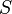 is the start variable (or start symbol), used to represent the whole sentence (or program). It must be an element of
is the start variable (or start symbol), used to represent the whole sentence (or program). It must be an element of  .
.
Production rule notation
A production rulein 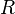 is formalized mathematically as a pair
is formalized mathematically as a pair 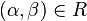 , where
, where 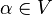 is a non-terminal and
is a non-terminal and  is a string of variables and/or terminals; rather than using ordered pair notation, production rules are usually written using an arrow operator with
is a string of variables and/or terminals; rather than using ordered pair notation, production rules are usually written using an arrow operator with  as its left hand side and
as its left hand side and  as its right hand side:
as its right hand side: 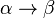 .
.
It is allowed for  to be the empty string, and in this case it is customary to denote it by ε. The form
to be the empty string, and in this case it is customary to denote it by ε. The form 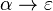 is called an ε-production.[4]
is called an ε-production.[4]
It is common to list all right-hand sides for the same left-hand side on the same line, using | (the pipe symbol) to separate them. Rules  and
and 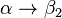 can hence be written as
can hence be written as 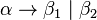 .
.
Rule application
For any strings  , we say
, we say  directly yields
directly yields  , written as
, written as 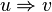 , if
, if 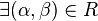 with
with 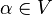 and
and 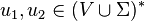 such that
such that  and
and  . Thus,
. Thus,  is the result of applying the rule
is the result of applying the rule  to
to  .
.
Repetitive rule application
For any 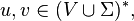 we say
we say  yields
yields  written as
written as 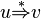 (or
(or  in some textbooks), if
in some textbooks), if  such that
such that 
Context-free language
The language of a grammar  is the set
is the set
A language 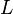 is said to be a context-free language (CFL), if there exists a CFG
is said to be a context-free language (CFL), if there exists a CFG 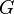 , such that
, such that 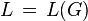 .
.
Proper CFGs
A context-free grammar is said to be proper, if it has
- no inaccessible symbols:
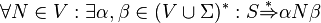
- no unproductive symbols:
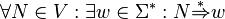
- no ε-productions:
 ε
ε
(the right-arrow in this case denotes logical “implies” and not grammatical “yields”) - no cycles:

Example
The grammar 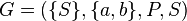 , with productions
, with productions
- S → aSa,
- S → bSb,
- S → ε,
is context-free. It is not proper since it includes an ε-production. A typical derivation in this grammar is
- S → aSa → aaSaa → aabSbaa → aabbaa.
This makes it clear that 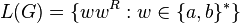 . The language is context-free, however it can be proved that it is not regular.
. The language is context-free, however it can be proved that it is not regular.
